DNA indeholder enorme mængde kode, som bruges, når proteiner skal produceres i en celle. Men hvor kommer koden fra? Kan den opstå tilfældigt, eller står der en intelligens bag?

Store tal

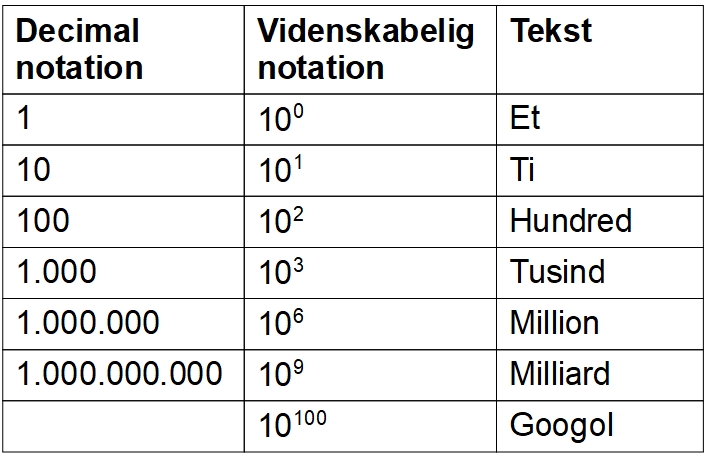
Figuren ovenfor viser eksempler på videnskabelige notation som bruges, når man vil skrive store tal på en nem måde.

Eksempel med mikrocontroller

Jeg har arbejdet med kodning af mikrocontrollere (små computere) i mange år. Her bruger man det binære talsystem, som består af 0 og 1. De to tal kan bruges til kodning, fordi de anbringes i en bestemt rækkefølge. Her følger et eksempel på kodning af en mikrocontroller ved hjælp af det binære talsystem.

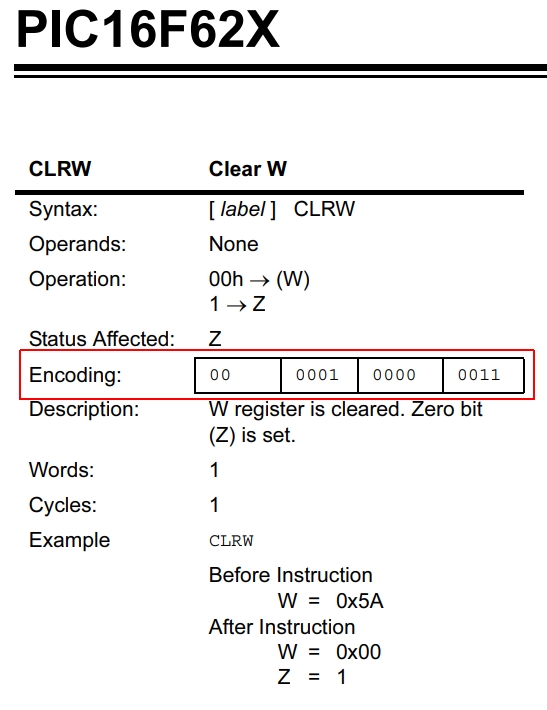
Koden ses i den røde ramme på figur 2, og den består af disse 14 tal: 00000100000011. Netop denne kode bevirker, at mikrocontrolleren gør en bestemt ting. Her er det registeret W, som bliver nulstillet. En sådan kode kaldes for en instruktion, nærmere betegnet en ”14-bit instruktion” da den indeholder 14 binære tal (bits).

Kan denne kode opstå af sig selv? Sandsynligheden for, at det kan ske, er 1 ud af 2¹⁴. Det kan også skrives 1 ud af 16.384. Hvis man har 14 dominobrikker, og hver brik har værdierne 0 og 1, skal man kaste brikkerne op til 16.384 gange før koden dannes. Det kan altså lade sig gøre, hvis man er tålmodig og har god tid!

Det bliver straks sværere, hvis et helt program skal dannes ved tilfældigheder. Et normalt program til den lille computer på figur 2 har mindst 1000 instruktioner, og hvis 1000 instruktioner skal dannes tilfældigt, er sandsynligheden 1 ud af (2¹⁴)¹⁰⁰⁰ hvilket er det samme som 1 ud af 2¹⁴⁰⁰⁰.

En tommelfingerregel inden for sandsynlighedsregning siger, at sandsynligheder over 1 til 10⁵⁰ aldrig vil finde sted. Det er altså helt usandsynligt, at der ved et tilfælde kan dannes computerkode med 1000 instruktioner.

Eksempel med DNA

Lad os nu regne på et eksempel med DNA. Et gennemsnitligt protein består af ca. 300 aminosyrer. Lad os gå ud fra et mindre protein med 150 aminosyrer; det er nemmere at konstruere. Hvad er sandsynligheden for, at dette protein kan dannes ved en tilfældighed? For evolutionslæren forudsætter tilfældigheder og benytter sig ikke af intelligens.

Der er 20 forskellige aminosyrer, som kan indsættes i den kæde, som til sidst bliver til protein. På den første plads er der 20 muligheder. På første og anden plads er der 20² muligheder (400 muligheder). På de tre første pladser er mulighederne 20³ = 8.000. På alle 150 pladser er der 20¹⁵⁰ muligheder, hvilket er det samme som 1,427 x 10¹⁹⁵. Dette tal er ufatteligt stort, og det er helt udelukket, at tilfældigheder kan frembringe dette resultat.

Beregningerne ovenfor skal korrigeres, for de forudsætter dannelse af ét bestemt protein, som er sammensat af 150 aminosyrer. I virkeligheden kan mange forskellige proteiner med 150 aminosyrer dannes. Sandsynligheden for tilfældigt at danne et fungerende protein er altså gunstigere end beregnet ovenfor. Desuden skal foldning af den lange peptidkæde også indgå i beregningen. Det er nemlig ikke alle aminosyre-sekvenser, som lader sig folde.

Biokemikeren Douglas Axe udførte omfattende laboratorieforsøg på Cambridge University i England i 2004. Han kom frem til, at sandsynligheden for tilfældigt at danne et foldet, brugbart protein er 1 ud af 10⁷⁷. Det er dokumenteret i den videnskabelige artikel Estimating the Prevalence of Protein Sequences Adopting Functional Enzyme Folds. Tallet 10⁷⁷ er ufatteligt stort, og det er helt umuligt at opnå på tilfældig vis.

Ovenstående to afsnit er inspireret af side 94-96 i bogen Exit Evolution. Du kan se bogens forside på figur 3.

Shakespeare og den skrivende abe

“The infinite monkey theorem” lyder således: En abe, der taster tilfældigt på en skrivemaskine i uendelig lang tid, vil næsten helt sikkert indtaste en given tekst, for eksempel William Shakespeares “Hamlet”.

Den danske Wikipedia skriver følgende om The infinite monkey theorem: Hvis man ser bort fra tegnsætning, mellemrum og store bogstaver, vil en abe, som taster tilfældige bogstaver, have chancen én ud af 26 for korrekt at taste det første bogstav i Hamlet (hvis man begrænser sig til det engelske alfabet). Den har chancen én ud af 676 (26 gange 26) for at taste de første to bogstaver. Fordi sandsynligheden mindskes eksponentielt, vil den ved 20 bogstaver kun have chancen én ud af 26²⁰ hvilket nogenlunde svarer til chancen for at købe fire amerikanske lottokuponer efter hinanden og vinde den store præmie hver gang.

I tilfældet med hele teksten i Hamlet er sandsynlighederne så forsvindende små, at de knap er fattelige i menneskelig sammenhæng. Selv hvis man fjerner al tegnsætning, indeholder teksten i Hamlet mere end 130.000 bogstaver, hvilket fører til en sandsynlighed på én ud af 3.4×10¹⁸³⁹⁴⁶. Til sammenligning er der kun omkring 10⁷⁹ atomer i det synlige univers, og der er kun gået 10¹⁷ sekunder siden Big Bang. Citat slut.

Konklusion

Tilfældigheder kan frembringe en simpel kode, for eksempel 14 bit i det binære talsystem. Men det er usandsynligt, at tilfældigheder kan frembringe store computerprogrammer, DNA-sekvenser, proteiner og ”Hamlet”.

Kilder
Forsidefoto: Can Stock Photo/Eastphoto